Revised: Feb./7th/2005; Since: Mar./10/2003
知らなくても良いことですが、2 進数の基本を説明しておきます。
2 進数 (binary) とは、数を、0 と 1 だけで表現する方法です。通常使っているものには、2 進数 (binary)、8 進数 (octal)、10 進数 (decimal)、16 進数 (hexadecimal) などがあります。コンピュータでは使われませんが、12 進数は、時間/月などで使われ、ダース(12)/グロス(144=12×12)などの単位でも使われています。
10 進数は 0~9 までの 10 個の文字を使って表現し、8 進数は 0~7 までの 8 個の文字を使って表現し、 16 進数は 0~f までの 16 個の文字を使って表現します。
10 進数の場合は、9 を超える数は、桁上がりによって表現します。
1976 = 6×100 + 7×101 + 9×102 + 1×103
16 進数の場合は、0,1,2,3,4,5,6,7,8,9,a,b,c,d,e,f を超える数を、桁上がりによって表現します。
(7B8)16 = 8×160 + B (=11)×161 + 7×162
= 8 + 176 + 1792
= 1976
2 進数の場合は、1 を超える数を、桁上がりによって表現します。
(0111 1011 1000)2 = 0 × 20 + 0 × 21 + 0 × 22 + 1 × 23
+ 1 × 24 + 1 × 25 + 0 × 26 + 1 × 27
+ 1 × 28 + 1 × 29 + 1 × 210 + 0 × 211
= 0 + 0 + 0 + 8 + 16 + 32 + 0 + 128 + 256 + 512 + 1024 + 0
= 1976
極単純に、桁上がりによってカウントアップすると、2 進数と他の進数を併記したものは、次のようになります。
binary | octal | decimal| hexadecimal ---------+--------+--------+------------ 0000 | 00 | 00 | 00 0001 | 01 | 01 | 01 0010 | 02 | 02 | 02 0011 | 03 | 03 | 03 0100 | 04 | 04 | 04 0101 | 05 | 05 | 05 0110 | 06 | 06 | 06 0111 | 07 | 07 | 07 1000 | 10 | 08 | 08 1001 | 11 | 09 | 09 1010 | 12 | 10 | 0a 1011 | 13 | 11 | 0b 1100 | 14 | 12 | 0c 1101 | 15 | 13 | 0d 1110 | 16 | 14 | 0e 1111 | 17 | 15 | 0f
コンピュータでの数の表現には、他にも、ゾーン10進数 (zone decimal)、パック10進数 (packed decimal) などが使われています。
Javaでは、負の符号付整数を表現するのに、2の補数 (2's complement) を使います。
先に説明したとおり、正の数は次のように表現されます。ここでは byte 型の 8 ビット(1 バイト)の例を挙げます。
2進数 10 16 ------------------- 0000 0000 00 00 0000 1000 08 08 0001 0000 16 10 .... 0000 0001 01 01 0000 1001 09 09 0001 0001 17 11 0000 0010 02 02 0000 1010 10 0a 0001 0010 18 12 0000 0011 03 03 0000 1011 11 0b 0001 0011 19 13 0000 0100 04 04 0000 1100 12 0c 0001 0100 20 14 0000 0101 05 05 0000 1101 13 0d 0001 0101 21 15 0000 0110 06 06 0000 1110 14 0e 0001 0110 22 16 0000 0111 07 07 0000 1111 15 0f 0001 0111 23 17
負の数を表現するのに2の補数というものを使います。そもそも、補数というのは、ある基準となる数から引いた数のことです。
その桁内の最大の数から引いた数を1の補数と呼びます。
1111 1111 - 0100 1010 ------------ 1011 0101 <- 1の補数
その桁内の最大の数+1から引いた数を2の補数と呼びます。
1111 1111 - 0100 1010 + 0000 0001 <- 2の補数にするために1加える ------------ 1011 0101 + 0000 0001 ------------ 1011 0110 <- 2の補数
2進数における1の補数は、単純にビット反転しただけのものになります。これに1加えたものが2の補数です。
0100 1001 ---------- 1011 0110 <- 1の補数 1011 0111 <- 2の補数
Javaに限らず、一般に整数の負数は、正数の2の補数を使います。
0111 1111 +127 <- 先頭ビットだけが0だと、そのビット内で最大の正の整数 0111 1110 +126 .... 0000 0101 +5 0000 0100 +4 0000 0011 +3 0000 0010 +2 0000 0001 +1 <- 先頭ビットが0だと正の整数 ---------------- 0000 0000 0 ---------------- 1111 1111 -1 <- 全て1だと、ビットに寄らず-1 1111 1110 -2 <- 先頭ビットが1だと負の整数 1111 1101 -3 1111 1100 -4 1111 1011 -5 .... 1000 0010 -126 1000 0001 -127 1000 0000 -128 <- 先頭ビットだけが0だと、そのビット内で最小の負の整数
ここで見るとおり、負数は最初のビットが1になり、正数は0になります。また、負数の最小値は-128(2の7乗)であり、正数の最大値は127になることもわかります。
データサイズによらず、整数の場合は、全てのビットが1である場合は-1を表します。これは覚えておくべき事柄です。
一般に、プログラミング言語では、小数は浮動小数点数 (Floating point numbers) と呼ばれる形で表します。32 ビット表現を単精度 (single precision) と呼び、64 ビット表現を倍精度 (double precision) と呼びます。
浮動小数点数は、ぶっちゃけた話、指数表現で数を表すことです。
例えば、光の速さは、[m/sec.]単位で、2.99792458×108、アヴォガドロ定数は6.022×1023 [mol-1、個]。一方、電気素量は1.602×10-19 [C]、プランク定数は6.626×10-34 [J・s]です。これらを固定小数点数で表現しようとすれば、整数の桁に 40 個、小数の桁に 40 個で合わせて 80 桁のデータサイズが必要になります。しかも、問題なのは、80 桁全てに数字が必要かというと、有効数字は高々 10 桁程度。これより詳細な数値は誤差の範囲で無意味、即ち 80 桁中に有為な数は 10 個以下、残り 70 桁は 0 がずら~と続くわけです。
これではモッタイナイので、浮動小数点数では、有効数字 (significand) を 8 桁程度にして、莫大/莫小な数は指数 (exponent) で表現します。有効数字を表す有意な数は、ビットの一意性を保つために、整数部が一桁になるように正規化し、これを仮数 (mantissa) と呼びます。符号小数点数は、「符号、指数、仮数」のビット列で表現されます。
浮動小数点数の表現の一つである IEEE (Institute of Electrical and Electronics Engineews; 米国電子技術者協会、通称アイトリプルイー)の 754 規格では、一つの浮動小数点数を 32 ビットまたは 64 ビットで表現します。32 ビットを単精度 (Single Precision) と呼び、 64 ビットを倍精度 (Double Precision) と呼びます。これらの拡張形式を実装するように推奨し、相互運用や演算規則などが規定されています。
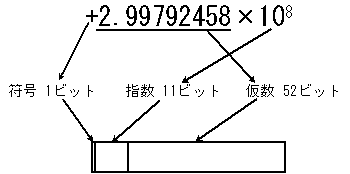
IEEE754 では、ビットの使い方として、符号 (sign)/指数 (exponent)/仮数 (mantissa)を次のように定義しています。
例えば、光の速さ 2.99792458×108 [m/sec.] では、2.99792458 が仮数、8 が指数です。
 |
| 図:IEEE 754規格倍精度浮動小数点数(数値は光速度[m/s]) |
|---|
JVM 内部では、浮動小数点数は単精度 float 型データが基本となっており、倍精度 double 型データは二つの float 型浮動小数点数の組み合わせとして表現されています。これは知らなくても良い JVM の内部ロジックの話であって、言語仕様としては、 3.14 などの単なる小数点数は double 型に認識されます。float 型で認識させたいときは、3.14F のように小数点数の末尾に F を付加して記述します。
単精度のビットパターンによる表現を紹介します。
単精度のIEEE 754浮動小数点数は、符号ビット(1 ビット)、指数部(8 ビット)、仮数部(23 ビット)の 32 ビットで表現されます。
指数部は 2 の 0 乗のとき、0111 1111となります。
指数部の二進数表現 ... 1000 0011 +4乗 1000 0010 +3乗 1000 0001 +2乗 1000 0000 +1乗 0111 1111 0乗 0111 1110 -1乗 0111 1101 -2乗 0111 1100 -3乗 ...
仮数部は 2 を基数として整数部が一桁になるように正規化した数の 2 進数表現になります。
正規化によって仮数部の最上位ビットは常に 1 になるので、実際に用意しておく必要はなく、倍精度の 52 ビットであれば、最上位の 1 を hidden bit にして含めなければ、53 ビット分の情報が含まれることになります。
小数の二進数表現 0.1000 1/2 = 0.5 0.0100 1/(2*2) = 0.25 0.0010 1/(2*2*2) = 0.125 0.0001 1/(2*2*2*2) = 0.0625
符号ビットは 1 ビットで、1 は負の数、0 は正の数を表します。
例えば、21.6875 = (0001 0101.1011)2 = (1.01011011)2×24となるので、指数部の 4 乗が 1000 0011 となり、仮数部は 1 .01011011000000000000000 となります。仮数部の最上位ビットの 1 を hidden bit にして含めなければ、結果として、単精度では "0 | 1000 0011 | 010 1101 1000 0000 0000 0000" となります。
次のコードで、 十進数の IEEE 754 浮動小数点表現が得られます。
FloatingPoint.java:
class FloatingPoint {
public static void main(String[] args) {
// 文字列 args[0] を float 型に変換
float f = Float.parseFloat(args[0]);
// float 型 f のビット表現を文字列 str に変換
String str = Integer.toBinaryString(Float.floatToRawIntBits(f));
System.out.println(args[0] + " = " + str);
}
}
C:\java>javac FloatingPoint.java C:\java>java FloatingPoint 21.6875 21.6875 = 1000001101011011000000000000000 C:\java>java FloatingPoint -21.6875 -21.6875 = 11000001101011011000000000000000
IEEE754 の "hidden bit" について、「かりや」さんにご教示いただきました。また、Float.floatToRawIntBits() での確認をお勧めいただきました。ありがとうございました。
| SEO | [PR] ����!�����u���O �����z�[���y�[�W�J�� �������C�u���� | ||
